学科知识 和 教学能力,这两者相辅相成,缺一不可。

第一部分:初中数学学科知识
扎实的学科知识是教学的根基,初中数学教师不仅要掌握初中阶段的知识,还要对小学和高中知识有连贯的理解,形成完整的知识体系。
(初中阶段“数与代数”、“图形与几何”、“统计与概率”)
A. 数与代数
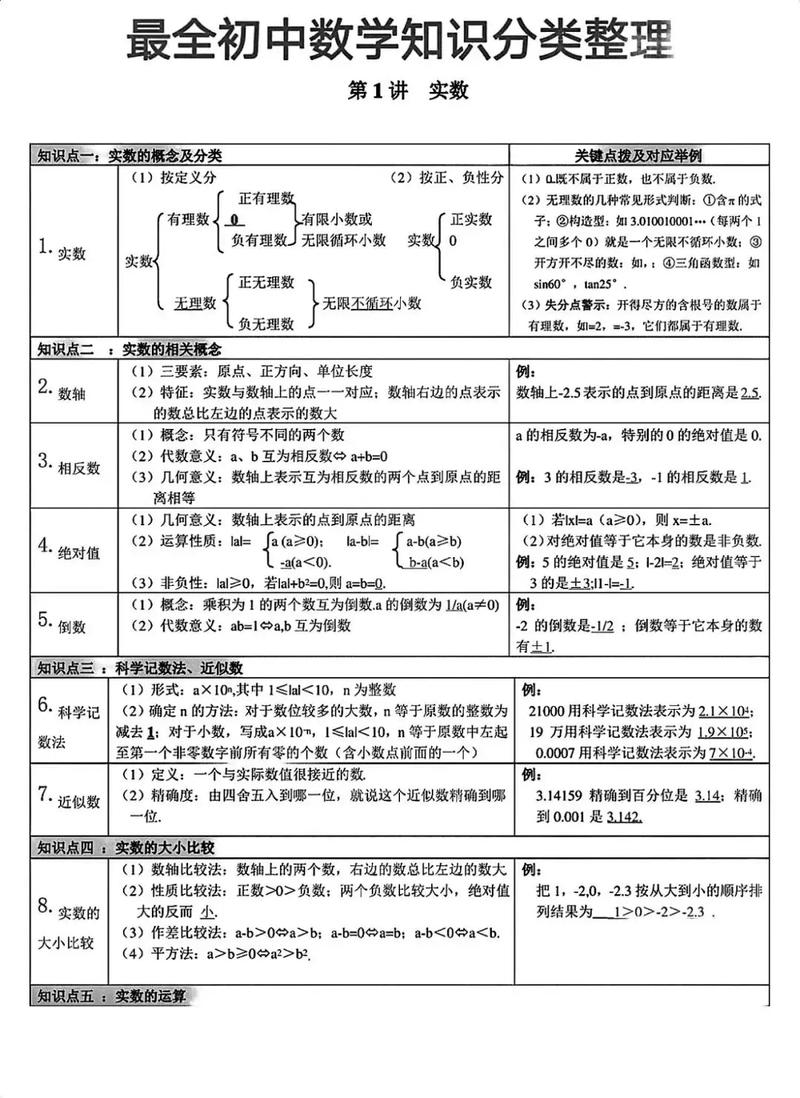
- 有理数与实数: 理解数轴、相反数、绝对值、倒数等概念;掌握有理数的四则运算、乘方、混合运算;理解无理数的概念,掌握实数的运算和大小比较。
- 代数式:
- 整式: 合并同类项、去括号、添括号、整式的加减乘除(特别是乘法公式:平方差、完全平方)。
- 分式: 分式的基本性质、运算。
- 二次根式: 二次根式的化简与四则运算。
- 方程与不等式:
- 一元一次方程/不等式: 解法与应用。
- 二元一次方程组: 解法(代入法、加减法)与应用。
- 一元二次方程: 解法(直接开平方法、配方法、公式法、因式分解法)、根的判别式、根与系数的关系(韦达定理)、应用。
- 分式方程与无理方程: 解法及验根。
- 函数:
- 一次函数: 图像与性质、k和b的意义、与方程/不等式的关系。
- 反比例函数: 图像与性质、k的意义。
- 二次函数: 图像与性质(开口方向、对称轴、顶点、增减性)、顶点式、交点式、与一元二次方程的关系、最值问题。
B. 图形与几何
- 图形的初步认识: 直线、射线、线段、角、相交线与平行线。
- 三角形:
- 概念、三边关系、内角和定理。
- 全等三角形(SSS, SAS, ASA, AAS, HL)。
- 等腰三角形、等边三角形的性质与判定。
- 勾股定理及其逆定理。
- 四边形:
- 平行四边形、矩形、菱形、正方形的性质与判定。
- 梯形的性质与中位线定理。
- 圆:
- 垂径定理、圆心角、圆周角定理及其推论。
- 点、直线、圆与圆的位置关系。
- 切线的性质与判定。
- 弧长、扇形面积、圆锥的侧面积和全面积。
- 图形的变换: 轴对称、平移、旋转、相似(位似)。
- 解直角三角形: 锐角三角函数(正弦、余弦、正切)、特殊角的三角函数值、解直角三角形的应用(仰角、俯角、坡角等)。
C. 统计与概率
- 统计:
- 数据的收集与整理(普查、抽样调查)。
- 数据的描述:平均数、中位数、众数、极差、方差、标准差;扇形统计图、条形统计图、折线统计图。
- 数据的分析:用样本估计总体。
- 概率:
- 事件与可能性。
- 概率的计算(列举法、列表法、树状图法)。
- 用频率估计概率。
学科素养与高观点
- 数学思想方法: 这是学科知识的灵魂。
- 数形结合思想: 如函数图像与性质的结合、几何问题代数化。
- 分类讨论思想: 如绝对值、含参数的方程、几何图形的多种情况。
- 转化与化归思想: 如将未知问题转化为已知问题(分式→整式,多元→一元,曲线→直线)。
- 函数与方程思想: 用运动和联系的观点看待问题。
- 模型思想: 将实际问题抽象为数学模型(方程模型、函数模型、几何模型)。
- 高观点下的初中数学:
- 高等数学的视角: 了解极限思想(如无限循环小数)、集合论思想(如方程的解集)、群论思想(如数系的扩展)等,能帮助教师更深刻地理解初中数学的本质,居高临下地处理教材。
- 数学史: 了解重要概念(如负数、无理数、函数)和定理(如勾股定理、韦达定理)的历史背景和发展过程,能增加课堂的趣味性和文化底蕴。
第二部分:初中数学教学能力
这是将学科知识转化为学生可理解、可接受、可应用的能力,是教学艺术的体现。
课程标准理解与教材分析能力
- 吃透《义务教育数学课程标准》: 这是教学的“宪法”,要明确:
- 课程目标: 知识与技能、过程与方法、情感态度与价值观。
- 核心概念: 数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识、创新意识。
- 内容要求与活动建议: 知道教什么、教到什么程度,以及如何教。
- 深入分析教材:
- 宏观层面: 理解整套教材的知识结构、编排逻辑和螺旋上升的体系。
- 微观层面: 精读每一节课,分析其:
- 地位与作用: 承上启下的关系。
- 教学目标: 具体、可操作、可检测。
- 重难点: 教学重点是什么?学生理解的难点在哪里?如何突破?
教学设计能力
这是将教学理念转化为具体教学方案的过程。
- 创设情境: 设计能激发学生兴趣、引出数学问题的现实情境或数学情境。
- 设计问题串: 设计一系列有逻辑、有层次、能引导学生逐步深入探究的问题。
- 选择教学方法: 灵活运用讲授法、讨论法、探究式学习、合作学习、启发式教学等。
- 设计教学活动: 如小组合作、动手操作、数学实验、课堂游戏等。
- 板书设计: 条理清晰、重点突出、图文并茂,是微型教案。
- 例习题设计: 由浅入深,有基础巩固题、能力提升题、拓展探究题,体现层次性和思维量。
课堂教学实施能力
这是教学设计的现场呈现。
- 语言表达能力: 语言准确、精炼、生动、富有启发性,避免口头禅和科学性错误。
- 提问与互动技巧: 提问有效,能启发思考;组织好课堂讨论,关注不同层次学生的参与。
- 信息技术应用能力: 熟练使用几何画板、PPT、希沃白板等工具,动态展示几何图形、函数图像,使抽象数学直观化。
- 课堂组织与管理能力: 营造积极、民主、有序的课堂氛围,有效处理课堂生成性问题。
- 数学思想方法的渗透能力: 在知识传授过程中,潜移默化地引导学生体会和运用数学思想方法。
学业评价与反馈能力
- 评价方式多元化: 不仅关注纸笔测验,还要关注课堂观察、作业分析、项目报告、数学日记等过程性评价。
- 全面化: 不仅评价知识技能,还要评价学生的思维过程、合作精神、创新意识。
- 有效反馈: 作业批改和考试后,能给予学生具体、有针对性的反馈,帮助学生找到问题根源,并提出改进建议。
教学反思与研究能力
- 教学反思: 课后及时反思自己的教学设计、教学过程和教学效果,成功之处在哪里,不足之处是什么,如何改进,这是教师专业成长的核心途径。
- 教学研究: 参与教研活动,听课、评课,阅读教育教学文献,尝试进行小课题研究,不断提升自己的专业水平。
学科知识与教学能力的融合
一个优秀的初中数学教师,绝不是“知识的搬运工”或“解题的机器”。

- 知识是基础,能力是桥梁。 没有扎实的知识,教学就是无源之水;没有高超的教学能力,知识就难以被学生吸收。
- 融合的体现:
- 在讲“勾股定理”时,不仅能证明它,还能设计一个动手操作活动,让学生通过拼图去“发现”它,并感受其中蕴含的“转化”与“数形结合”思想。
- 在讲“函数”时,不仅能画出图像,还能联系生活中的实例(如手机套餐、行程问题),让学生建立函数模型,体会函数的价值。
- 在讲“一元二次方程”时,不仅能用公式法求解,还能引导学生探究“为什么要配方?”“韦达定理揭示了什么秘密?”,激发学生的探究欲。
“初中数学学科知识与教学能力” 的目标,是帮助学生“会数学、爱数学、用数学”,让他们在获得数学知识的同时,思维能力得到锻炼,科学精神得到培养,并感受到数学的严谨与美。