扎实的学科知识、高超的教学能力、以及持续的专业发展能力。
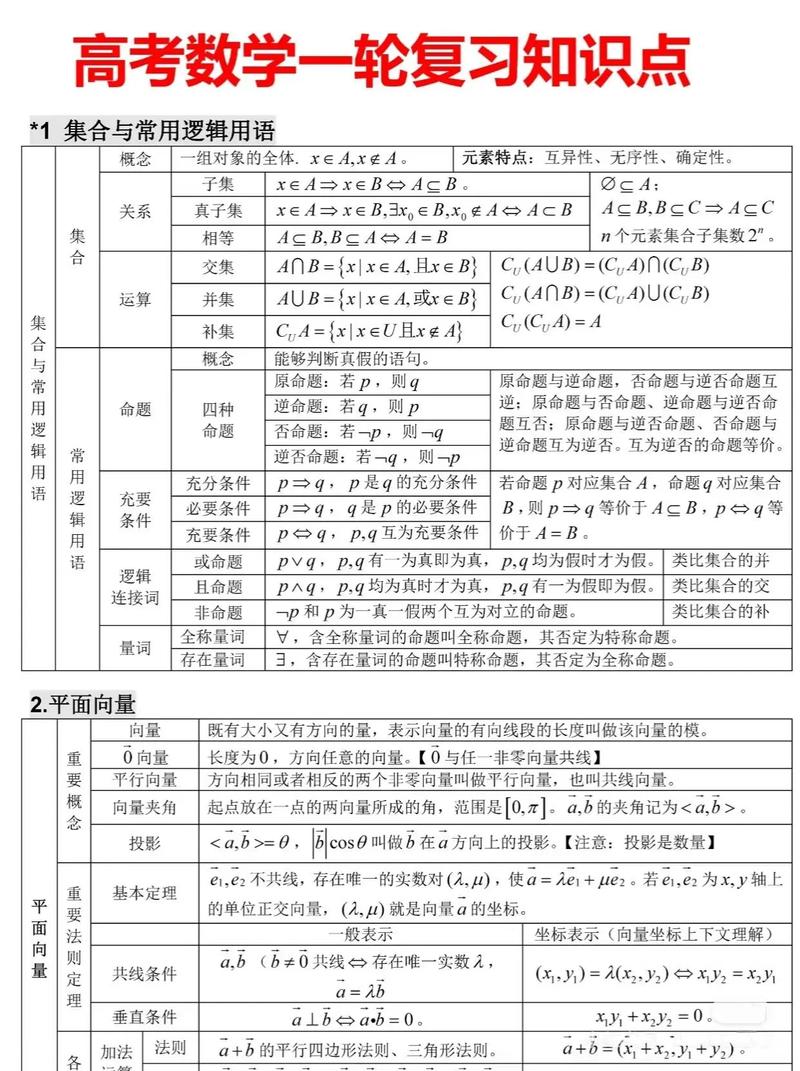
扎实的学科知识
这是作为一名数学教师的立身之本,它要求教师不仅要“知其然”,更要“知其所以然”,形成一个结构化、网络化、深度化的知识体系。
广博而严谨的数学基础
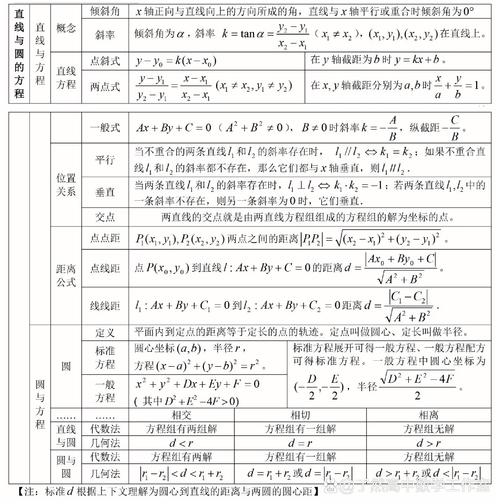
- 核心知识模块的精通: 对高中数学的各个模块(如集合与逻辑、函数、三角函数、数列、不等式、立体几何、解析几何、概率与统计、导数及其应用等)有深刻、准确的理解,能够清晰阐述每个概念的定义、内涵、外延以及与其他知识的联系。
- 知识体系的构建: 能够站在整个中学数学乃至高等数学的高度,审视高中知识点,讲函数时,能联系到大学的“映射”概念;讲数列极限时,能微积分中的“极限”思想;讲解析几何时,能体会到其与线性代数中“向量”和“矩阵”的关联,这种“高观点”下的俯视,能让教学更有深度和前瞻性。
- 数学思想方法的掌握: 高中数学的灵魂在于思想方法,教师必须深刻理解并能在教学中渗透:
- 函数与方程思想: 用运动和联系的观点看问题,将非函数问题转化为函数问题。
- 数形结合思想: 代数问题几何化,几何问题代数化,这是解析几何的核心。
- 分类讨论思想: 面对复杂问题时,根据其本质属性进行逻辑划分,逐个击破。
- 转化与化归思想: 将未知问题转化为已知问题,复杂问题转化为简单问题。
- 特殊与一般思想: 从特殊到猜想,再到一般性证明。
深厚的数学史与数学文化素养
- 了解背景: 知道重要数学概念、定理、公式(如勾股定理、二项式定理、微积分基本定理)的来龙去脉、历史背景和数学家的故事。
- 丰富教学: 在教学中融入数学史,可以激发学生的学习兴趣,让他们明白数学不是一堆冰冷的公式,而是人类智慧的结晶,是充满探索和创造的文化,讲复数时,可以介绍卡丹诺的“三次方程求根”和欧拉公式的优美。
扎实的解题能力与数学思维
- 解题“多”与“精”: 教师需要做远多于学生的题目,包括高考真题、模拟题、竞赛题(如一试难度)等,这不仅能保持手感,更重要的是能见识各种题型、解法和思维陷阱。
- 解法“优”与“通”: 面对一道题,教师不应只满足于一种解法,而要能迅速找到多种解法,并比较其优劣(如计算量大小、思维难度等),提炼出通性通法,让学生学会“以不变应万变”。
- 反思与归纳: 解题后要进行反思,这道题考察了哪些知识点?蕴含了什么思想方法?易错点在哪里?能否进行变式或推广?这种“解题-反思-归纳”的能力是提升教学针对性的关键。
高超的教学能力
这是将教师的学科知识“变现”为学生能力的关键环节,体现了教师的“教学智慧”。
教学设计能力
- 目标设定: 能够根据课程标准和学情,准确设定“知识与技能”、“过程与方法”、“情感态度与价值观”三维目标,并使目标具体、可操作、可检测。
- 过程设计: 设计出逻辑清晰、环节紧凑、层层递进的教学流程,能够创设有效的教学情境(如从生活实例、数学史、旧知复习等引入),激发学生探究欲望。
- 活动设计: 设计多样化的学生活动,如小组讨论、合作探究、上台展示、动手操作等,让学生成为课堂的主体,而非被动的听众。
课堂实施与驾驭能力
- 语言表达: 数学语言要准确、精炼、严谨,同时也要生动、形象、富有启发性,能用学生听得懂的语言解释抽象的数学概念。
- 提问技巧: 提问是引导思维的艺术,教师要会问“是什么”(确认事实)、“为什么”(探究原因)、“怎么样”(评估价值)、“还有什么”(拓展延伸)等不同层次的问题,激发学生深度思考。
- 生成性资源利用: 课堂是动态的,学生的回答、错误、困惑都是宝贵的教学资源,教师要有敏锐的洞察力,及时捕捉并利用这些“意外”生成新的教学点,将课堂引向深入。
- 信息技术融合: 熟练运用几何画板、GeoGebra等动态数学软件,以及PPT、希沃白板等工具,将抽象的数学关系可视化、动态化,帮助学生直观理解。
学情分析与因材施教能力
- 诊断学情: 通过作业、测验、课堂观察、个别交流等方式,准确把握班级整体水平和不同学生的个体差异(知识漏洞、思维特点、学习习惯等)。
- 分层教学: 在教学目标、教学内容、作业布置和评价方式上,对不同层次的学生提出不同要求,让“优等生吃得饱,中等生吃得好,学困生吃得了”,实现个性化发展。
评价与反馈能力
- 多元评价: 评价不应只有期末考试,要注重过程性评价,如课堂表现、作业质量、项目报告、数学日记等,全面了解学生的学习状况。
- 有效反馈: 作业和试卷的批改不应只是一个“√”或“×”,要写下针对性的评语,指出错误原因,肯定闪光点,给出改进建议,让学生明确努力的方向。
持续的专业发展能力
教育在发展,知识在更新,优秀的教师必须是一个终身学习者。
教学研究能力
- 问题意识: 能够从日常教学实践中发现问题,如“为什么学生总是记不住三角函数诱导公式?”“如何提高学生解析几何的运算准确率?”
- 行动研究: 针对问题,学习相关理论,设计教学方案(如设计一个“探究式”的诱导公式教学课),进行教学实践,观察效果,反思总结,形成研究报告或论文。
课程开发与整合能力
- 开发校本课程: 基于学校特色和学生需求,开发如“数学建模入门”、“趣味数学与逻辑游戏”、“数学史选讲”等选修课程或社团活动。
- 跨学科整合: 能够将数学与物理、化学、信息技术、经济、艺术等其他学科知识进行整合,设计出跨学科主题学习活动,培养学生的综合素养。
反思与总结能力
- 教学反思: 坚持撰写教学后记或教学反思,记录成功之处、败笔之处、学生的奇思妙想以及自己的感悟,这是教师成长最直接、最有效的途径。
- 经验交流: 积极参与校内外教研活动、公开课、教学比赛,虚心向同行学习,分享自己的经验,在交流碰撞中提升自我。
高中数学教师的“学科知识与能力”是一个“知识-能力-发展”三位一体的有机整体。
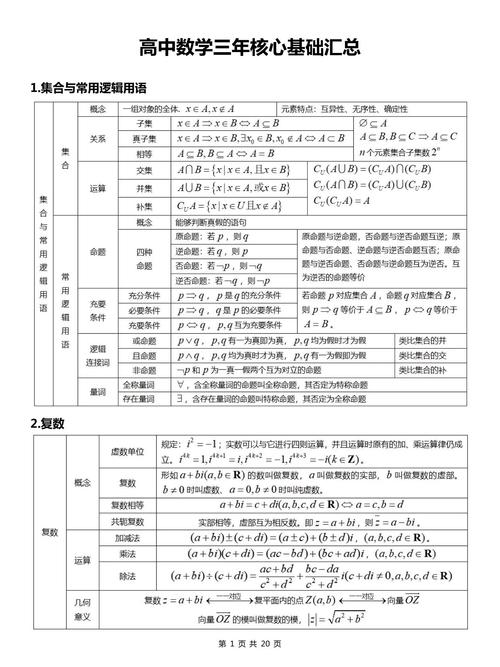
- 扎实的学科知识是基础,决定了教学的深度。
- 高超的教学能力是核心,决定了教学的效度。
- 持续的专业发展能力是保障,决定了教师职业生涯的长度和高度。
一个优秀的数学教师,既是数学知识的“专家”,也是学生思维的“引路人”,更是教学研究的“探索者”,他/她能用自己的专业素养和教学热情,点燃学生对数学的热爱,帮助他们建立起严谨的逻辑思维,并用数学的眼光去观察和改造世界。